There has been numerous speculations and attempts to calculate/guess what is the actual pixel per degree (PPD) of the Pimax headset. I took it as an opportunity to figure out the following method, which can provide a technical answer.
I will use:
- Pimax 5k+ headset (PiTool v1.0.1.91, FW v181)
- Normal FOV (but it should not matter as will be explained later)
- Parallel projection off
I will also use the results from the following threads:
- Transformed and pre-lens warped images from (https://community.openmr.ai/t/pimax-native-projection-and-pre-lens-warp-transformation/15775)
- Projection geometry for Normal FOV from (https://community.openmr.ai/t/all-the-different-fovs-of-pimax-5k/16053)
How to calculate PPD
Jump to the conclusion, if you are not interested in the calculation.
The idea is to calculate (or measure) the number of pixels used to display (some) defined viewing angle (FOV) and then just divide the former by the latter. I have already recorded the transformed static image as well as its warped version for the left eye.
The transformed static image:
The warped static image (i.e. what is actually displayed in the headset):
The red dots are marking the point where the view axis passes through the projection plane. These coordinates are calculated from the left eye projection geometry (for the Normal FOV):
Left eye (Normal FOV, PP off)
tan_left=-1.742203, tan_right=1.346154, tan_bottom=-1.269841, tan_top=1.269841
atan_left=-60.14°, atan_right=53.39°, atan_bottom=-51.78°, atan_top=51.78°
horizontal=3.09, vertical=2.54, aspect=1.22
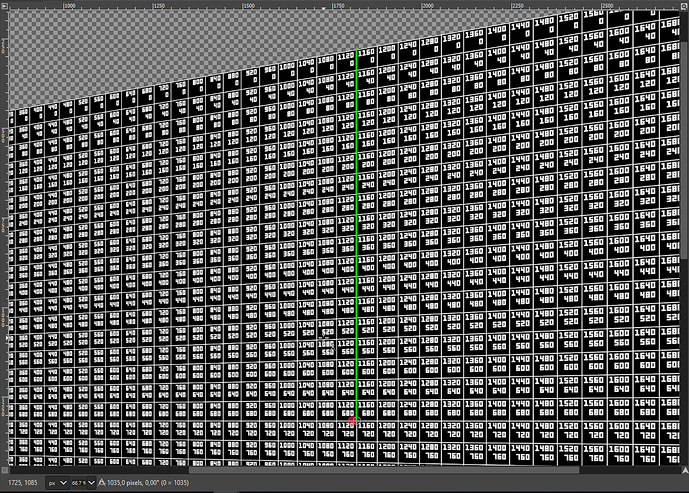
The coordinates are calculated in the transformed image this way:
x_size = 3202, y_size = 2633 (render target resolution for Normal FOV, PP off)
x = - tan_left / (tan_right - tan_left) * x_size = ~ 1806
y = - tan_bottom / (tan_top - tan_bottom) * y_size = ~ 1316
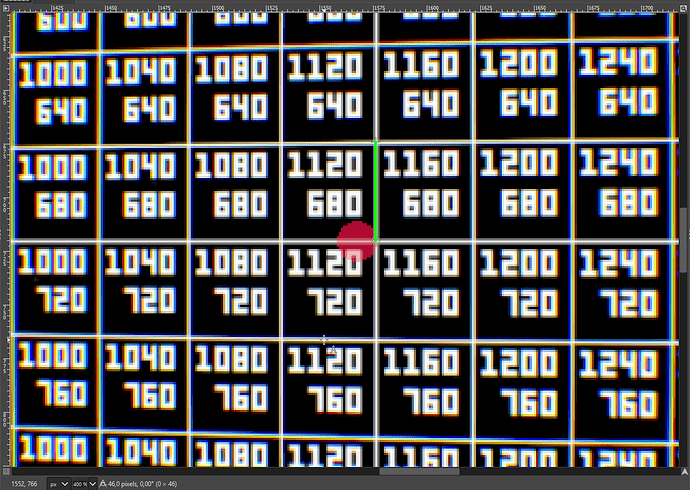
In the warped image the point is determined by the similarity (using the square grid and its “virtual coordinates”), its precise position is defined by the lens optical property and cannot be calculated from the known data.
Knowing the “central” point, we can measure the length of the side of the adjacent square. Let’s measure the vertical length as the squares seems to be symmetrically deformed, so we could assume that the PPD is more a less the same in both directions (horizontal and vertical). This will also allow us to apply the results to the other FOVs (Small and Large) as they do not differ in the vertical FOV from the Normal one:
The (vertical) length is sq_size=57 pixels.
We can also calculate the corresponding viewing angle, since we know the total FOV (tan_top=1.269841) and total pixel size (px_top=1316):
sq_fov = atan(sq_size/px_top * tan_top) = ~ 3,15°
Now we can measure the size of the same square after the warp transformation:
which is warp_sq_size=46. Since we already know that this square is observed at sq_fov angle, we can calculate the true PPD:
sq_ppd = warp_sq_size / sq_fov = ~ 14,6 PPD
This gives the PPD at the optical center, but the value is apparently not the same over the whole vertical range. To get an idea how much it changes, we can calculate the overall PPD for the “half” height of the static grid, by using the same approach as above, but measuring the length from the center to the top of the grid:
The transformed image gives the grid_height=1035 pixels. The warped grid height is warp_grid_height=663 pixels:
Using the similar formulas as before, we can calculate the corresponding FOV and the overall PPD for the whole section:
grid_fov = atan(grid_height/px_top * tan_top) = ~ 44,95°
grid_ppd = warp_grid_height / grid_fov = ~ 14,1 PPD
So we can see that in the vertical FOV of ~ 90° (=2*44,95°) the PPD does not change much and remains > 14,1 PPD.
We can assume the similar results for horizontal resolution, at least in the central area, which looks symmetrical.
Conclusion
The best PPD value = 14,6 PPD (center of the view/lens)
The average PPD value = 14,1 PPD (for 90° vertical FOV ~ horizontal)
The best PPD value corresponds to the center of the view (which corresponds to the center of the lens). Due to the symmetry we may assume that the PPD inside the 90° “cone” (horizontal or vertical) is larger than 14,1 PPD.