Following several posts on IPD settings problem and complains about the mismatch between measured distance between the lenses’ centers and the IPD reported by the headset I tried to figure out from where the problem comes and if it is even a problem.
I have been running recently some tests on ED and during those test I realized that it is relatively easy to play with OpenVR (using pyopenvr). I could get for example recommended rendering target resolution to prove that OpenVR applies the additional limit on the size which is not visible in the SteamVR UI (Elite Dangerous Setup Guide - Lets make it Dark Again :) - #131 by risa2000)
Another interesting info which one can get this way is what OpenVR calls Eye to head transform matrix by calling this function IVRSystem::GetEyeToHeadTransform.
This transformation matrix defines how the “eye coordinates” transform to the “head coordinates” and is used to split the original view (which would use the pancake version of the game) into the two views needed for stereo view rendering in VR.
When using PiTool in Compatible with parallel projection mode, the corresponding matrices read:
Left Eye:
[[ 1. , 0. , 0. , -0.03486158],
[ 0. , 1. , 0. , 0. ],
[ 0. , 0. , 1. , 0. ]]
Right Eye:
[[1. , 0. , 0. , 0.03486158],
[0. , 1. , 0. , 0. ],
[0. , 0. , 1. , 0. ]]
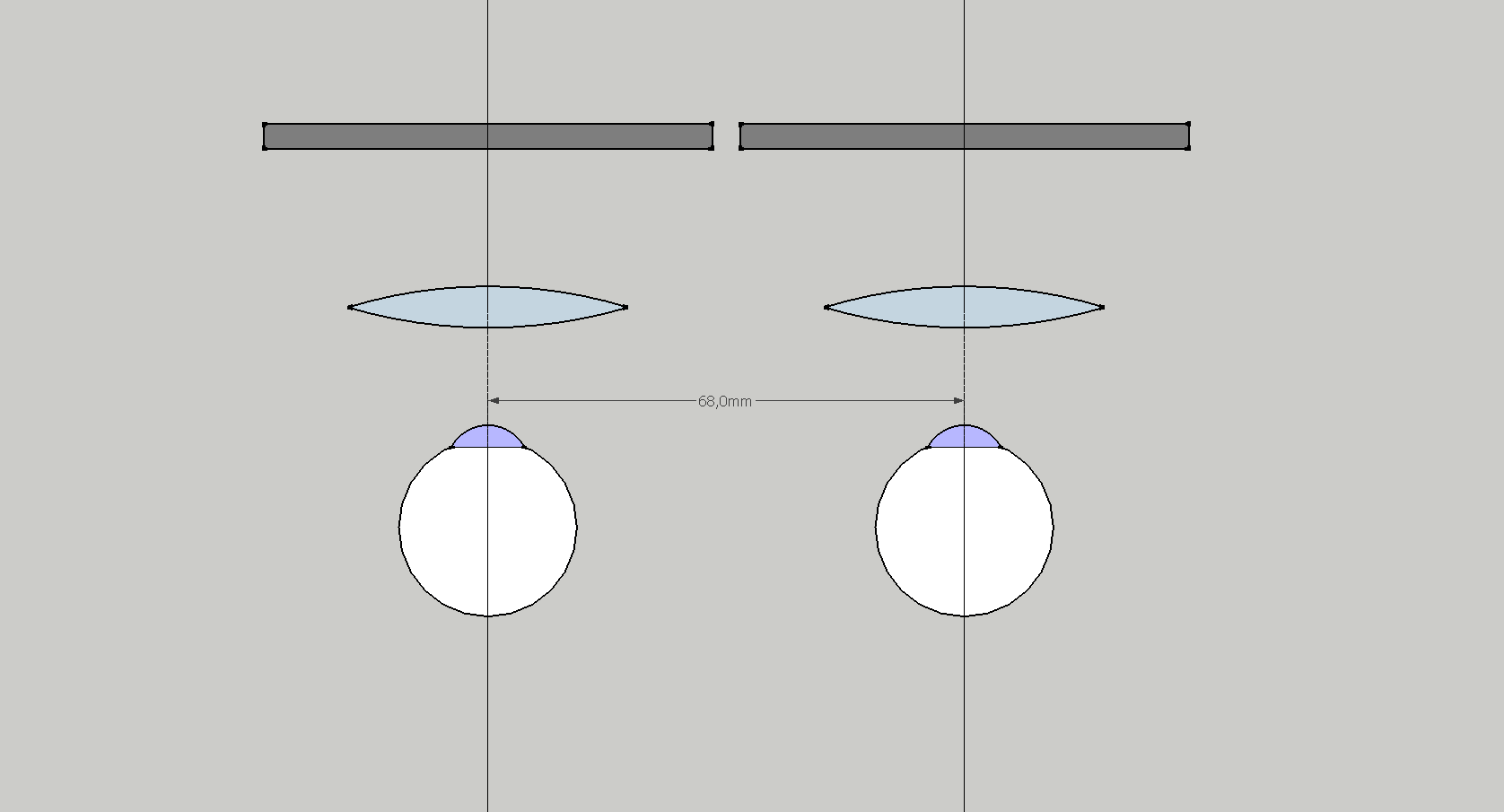
They look almost like an identity except the last column, which defines the translation and corresponds to the left and right eye offsets respectively. In this case it means I have my IPD set to ~ 70 mm and it is evenly split between the both eyes. (It is a translation defined along the X axis of the view space).
So far nothing new here, with the parallel projection enabled we are rendering to two coplanar views, which only differ by the shift along the X axis, the same way as for Rift or Vive.
Then I turned off “parallel projection” and read the matrices again in the native mode. The results got more interesting:
[[ 0.9848078 , 0. , 0.17364816, -0.03486158],
mLeft = [ 0. , 1. , 0. , 0. ],
[-0.17364816, 0. , 0.9848078 , 0. ]]
[[ 0.9848078 , -0. , -0.17364816, 0.03486158],
mRight = [ 0. , 1. , -0. , 0. ],
[ 0.17364816, 0. , 0.9848078 , 0. ]]
This shows not only translation along the X axis (which is the same), but also a rotation of the views. To demonstrate how to figure out the angle, I use the following direction vector
look = [0.0, 0.0, -1.0, 0.0]
in Eye view of the left eye. The first three numbers are the coordinates (X, Y, Z) and the last one is zero, because I am interested in direction transformation and not coordinates transformation (by putting 0 there, the translation is omitted, by putting 1 there it is included). Then calculating the new direction vector in Head coordinate system gives:
mLeft x look -> [-0.17364816, 0. , -0.9848078 ]
Since I know that the original vector had the length of 1, using this, the change of the X coordinate and basic trigonometry, I can calculate the angle of which the view rotated along the Y axis (this one does not change).
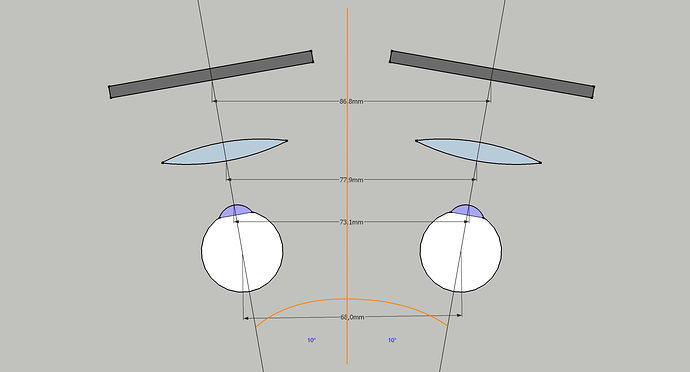
degrees(asin(0.17364816)) -> 9.999998972144015° ~ 10°
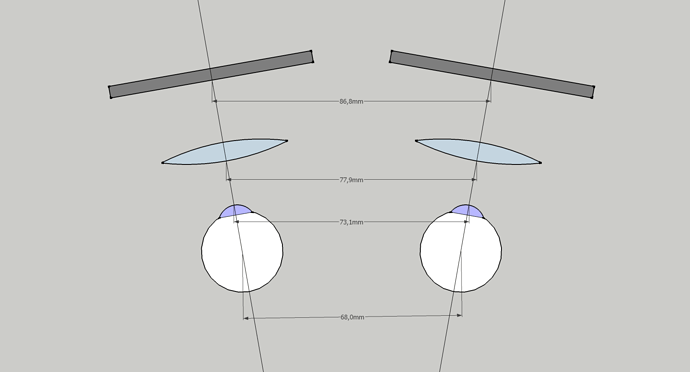
Which means that in the native “canted” mode, the views which the headset reports to the OpenVR are not parallel but divergent by 10° on each side.
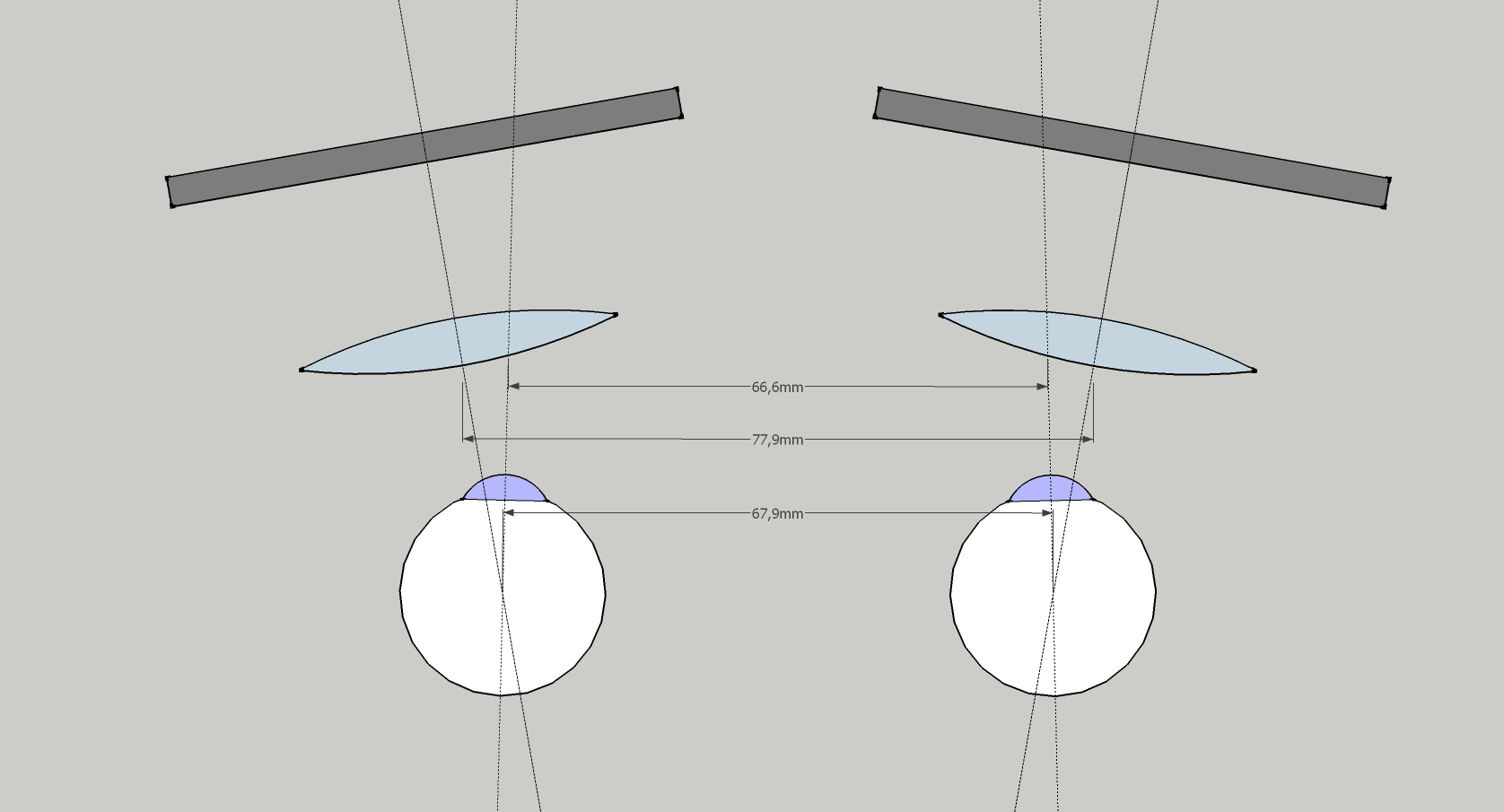
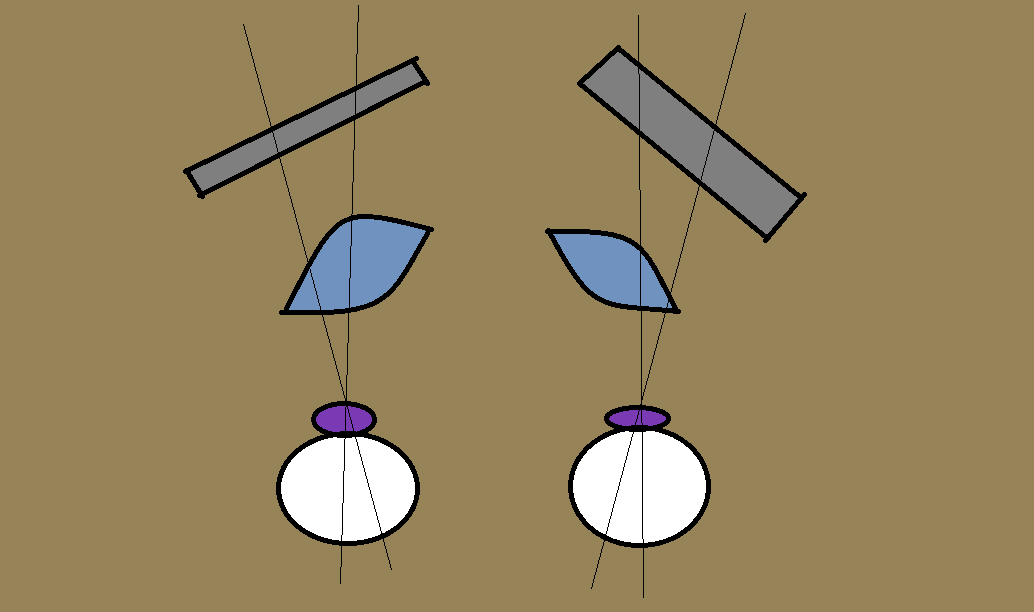
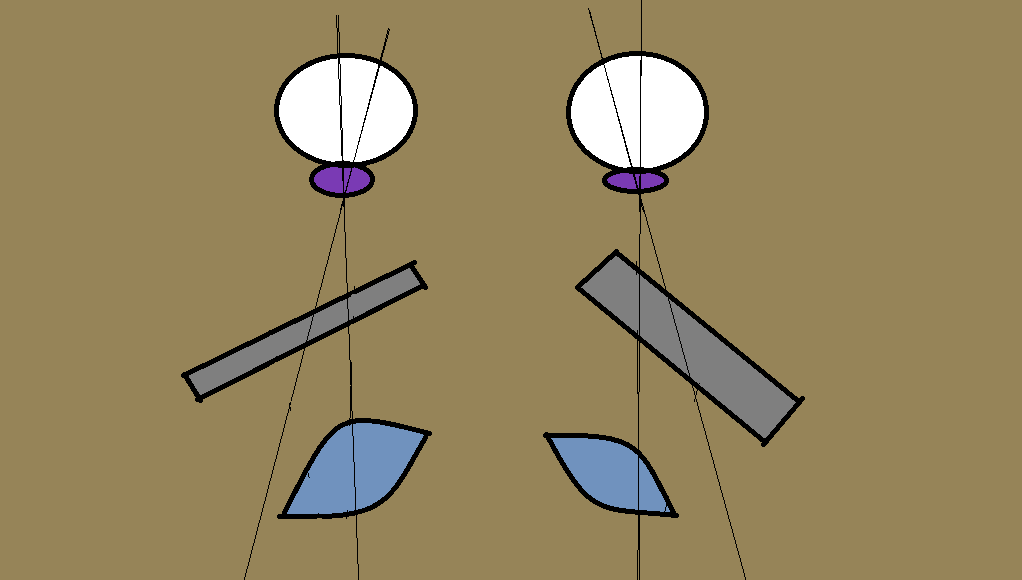
The visualization above is scale accurate to the eye size, IPD and the angle, but the placement of the lenses and panels are arbitrary, just to give an idea of the impact of the divergent property, notably how the lenses centers cannot be at the same distance as the eyes.
I also made an assumption, that the lenses are perpendicular to the optical axis (which corresponds to the view axis, reported by OpenVR) and that for the sake of a predictable behavior the lenses are positioned so that when the eye is looking through in the direction of the view defined by the headset, its optical axis is identical with the optical axis of the system.
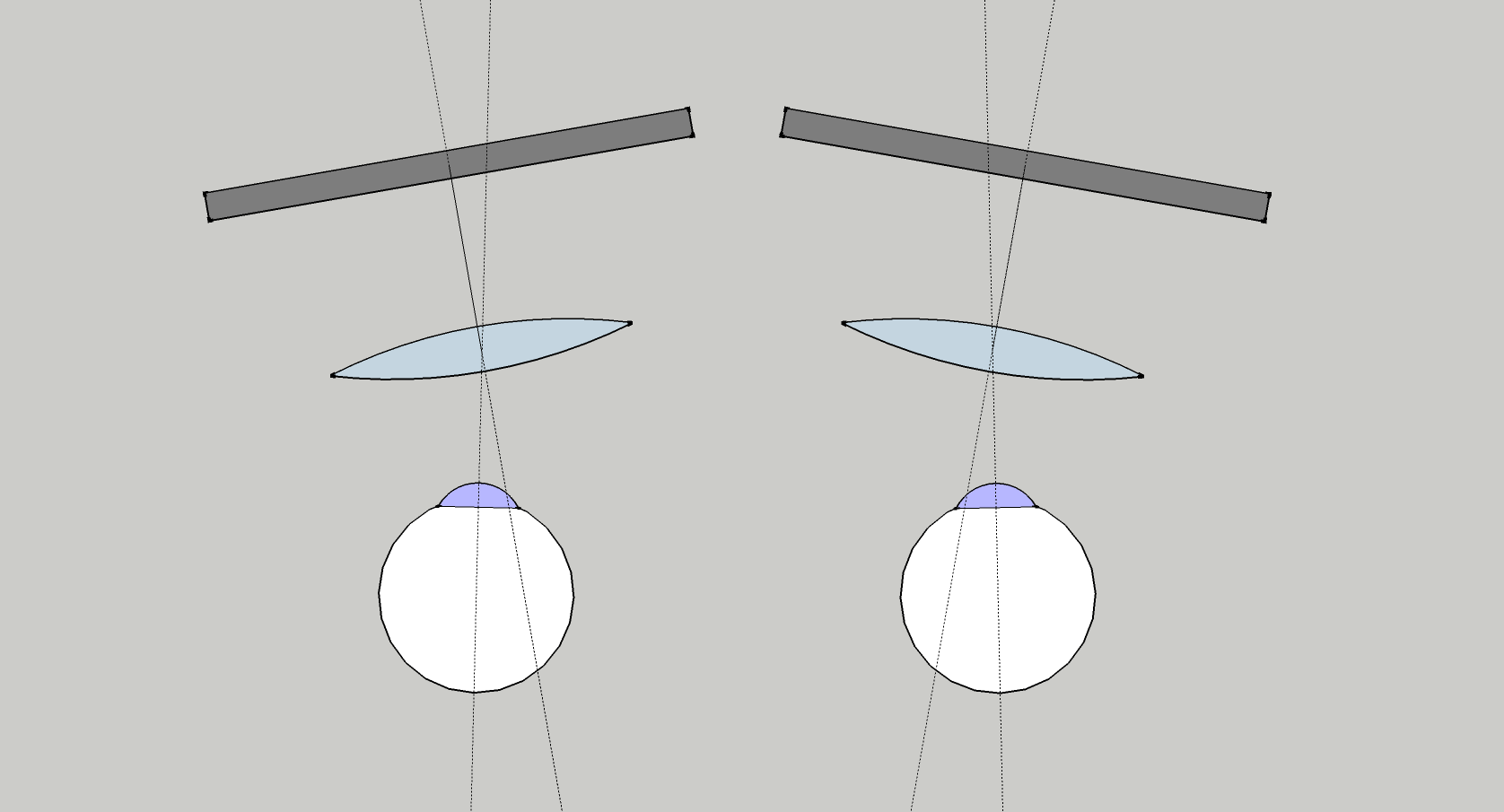
Now it should be easier to imagine what happens when you set the IPD lower than what is your real one. The optical axis gets offset but the angle remains the same, so you get the lenses centers closer to the IPD distance, at the cost of getting the angular offset slightly off.
The another consequence of this design is that thanks to the divergence of the views, the sweet spot becomes dependent on the distance from the face as it is no longer invariant as in the parallel projection. In paralel projection, if you set your IPD right you can move the headset further or closer and this will only change the FOV, in “canted” projection, moving the headset further or closer also changes the position of the sweet spot as it may end up in front of or behind the eye pupil.
I had it also on mind, but I had a feeling I had already overloaded the forum with my sketches.
